有许多同学写了统一省选d2t3,由于种种原因,当生成树个数在模意义下为0但存在生成树时会输出错误的答案。那么下面就让小编带大家一起了解一下如何生成一个在模意义下生成树个数为0的连通图。
我们考虑这样的一个构造,我们生成两个子图 $G_1$ 和 $G_2$,$G_1$ 和 $G_2$ 中前两个点都有一条边,我们考虑这两个图包含这条边的生成树个数和总生成树个数,记为 $(f_1,g_1),(f_2,g_2)$,那么我们考虑生成这样的一张图:
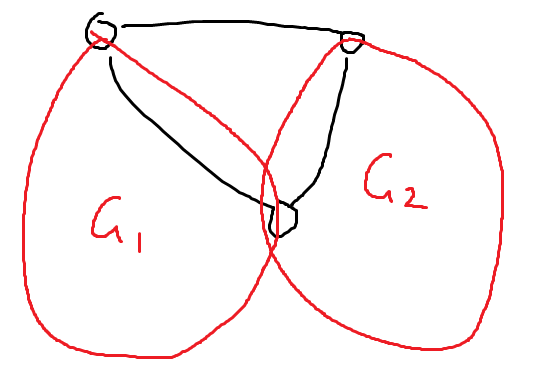
容易算出该图恰有 $f_1g_2+f_2g_1+g_1g_2=(f_1+g_1)(f_2+g_2)-f_1f_2$ 个生成树。$(f_1+g_1)(f_2+g_2)-f_1f_2\equiv 0$即$\frac{f_1+g_1}{f_1}\equiv \frac{f_2}{f_2+g_2}$。我们生成若干($O(\sqrt{mod})$)个随机图并meet in the middle即可。
下面附一组生成的数据,边权是在 $\{1,2\}$ 中随机的。
17 44
1 3 1
1 4 2
1 7 1
1 8 2
1 9 1
2 5 1
2 7 1
2 9 1
3 5 2
3 6 1
3 7 1
3 8 2
3 9 1
4 7 2
4 9 1
5 6 1
5 8 2
5 9 1
6 7 1
6 8 2
6 9 1
8 9 2
8 10 2
9 10 2
9 11 2
9 12 2
9 13 1
9 14 2
9 15 2
9 16 1
9 17 1
10 11 1
10 12 2
10 15 2
10 17 2
12 13 2
12 14 2
12 15 1
12 16 1
12 17 2
13 15 1
13 16 2
14 17 1
16 17 1这就是关于如何hack统一省选d2t3的事情了,大家有什么想法呢,欢迎在评论区告诉小编一起讨论哦!

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号